[Lecture 3] Probabilistic Robotics

본 포스팅은 양정연 교수님의 SLAM 수업을 Reference로 공부한 내용을 정리한 것입니다.

출처: Youtube, 양정연 교수님 SLAM

Stochastic & Probabilistic

로보틱스를 비롯한 여러 분야에서 주어진 문제를 해결하기 위한 방법론은 다양하게 제시되어 왔다. 지금까지 배워온 바에 의하면 문제를 모델링하고, 해당 모델을 관통하는 어떠한 수식이나 알고리즘을 사용하여 문제를 해결하는 것이 당연할 것이다. 하지만 이제는 새로운 방법론을 제안하고자 한다. 바로 확률에 기반한 방법론이다.

본격적인 진행에 앞서 강의에서 Stochastic한 상황을 설명하기 위해 앞선 강의에서 배웠던 경사 하강법(Gradient Descent)를 언급한다. 경사 하강법에서 local minima에 빠지는 경우와 global minima를 찾아가는 내용(찾을 수 없고, stochastic한 문제 상황에선 관심이 없다.)등에 대해 설명한다. 추가적으로 경사 하강법의 근본이 되는 미분이라는 방식의 한계점을 언급하며 새로운 최적화 방법론인 유전 알고리즘을 소개한다.

유전 알고리즘은 다양한 데이터 중 우월한 데이터를 교배시켜 더 나은 후손을 찾아보자는 아이디어에 기반한다. 하지만 이와 같은 방식에선, 선조 데이터들이 그다지 좋은 성능을 가지지 못한다면 그들의 유전자를 물려받은 후손은 더 나아지지 못한다는 한계를 가진다. 이를 타개하기 위한 트릭이 바로 돌연변이이다. 데이터들 중 우월한 유전자를 물려받은 일부와 랜덤한 노이즈 혹은 어떠한 조작을 거친 돌연변이들이 다음 세대를 구성하는 데이터가 된다. 이때 돌연변이는 기존 데이터의 성질을 그대로 이어가지 않고 더 발전할 수 있는 가능성을 가진다. 이렇게 수많은 세대와 돌연변이를 거치면서 최종적으로 가장 우월한 데이터를 얻어내는 것이 유전 알고리즘이다.

휴머노이드의 움직임, 센서, 모터의 출력 값 등 이외에도 몇 가지 예시를 들어가며 Stochastic한 환경, 문제에 대해서 설명을 해준다. 이들의 공통 분모는 바로 노이즈나 랜덤한 인풋에 따라 매 순간 완벽히 똑같은 모델이 존재하지 않는다는 것이다. 즉, 모든 액션은 확률에 기반한다.

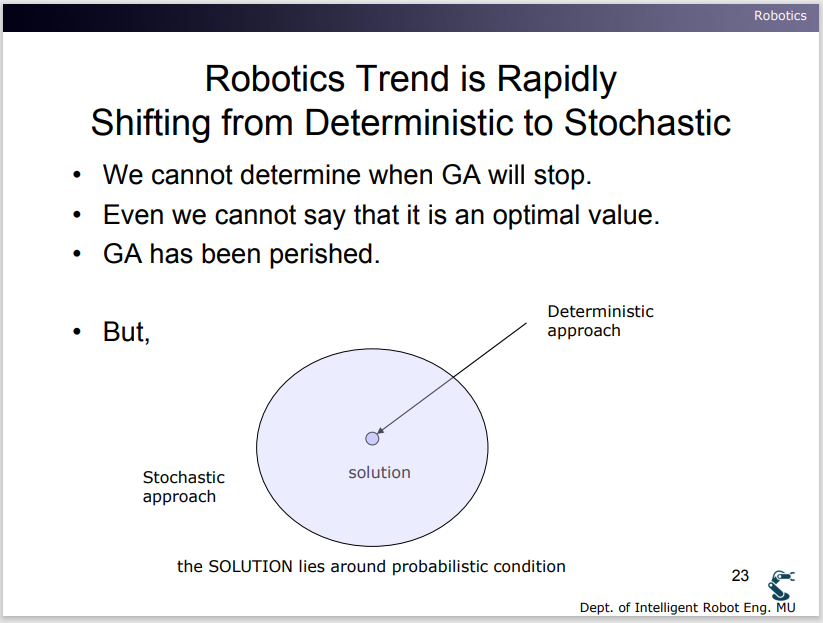
지금까지에 해당하는 내용은 다음 슬라이드에 함축적으로 정리돼 있는 듯 하다. Stochastics한 접근법은 완벽한 해답은 아니지만 실제 솔루션에 다가가기 쉽다는 것이다.

Stochastic Approach with Case Study

확률적인 솔루션에 대한 예시로 로봇 청소기를 소개한다. 로봇 청소기는 방 구석구석을 청소하기 위해 가능한 벽과 붙어서 이동해야 한다. 그렇다면 어떻게 벽을 따라 이동할 것인가? 라는 문제가 제기된다. 가장 먼저 떠오르는 방법으로는 단순 직진을 하다 정면에 벽이 있으면 90도 회전한 후 다시 직진하는 것이다.

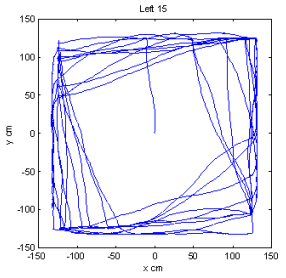
위와 같은 deterministic한 전략을 언뜻보면 완벽해 보일 수 있다. 하지만 이를 실제로 적용하면 절대 생각되로 되지 않는다. 바닥과의 slip이 존재할 것이고, 벽을 인식하기 위한 센서나 모터의 출력도 언제나 완벽하게 동일하지 않을 것이다. 이런 변수들로 인해 실제 시뮬레이션에서의 결과는 다음과 같다고 한다.

경로가 상당히 삐뚤어졌을 뿐 아니라 직진을 해야하는 구간에서도 제대로 직진을 하지 못한다. 물론 일부러 노이즈를 준 결과이긴 하지만 실제 로봇이라고 큰 차이가 있지는 않을 것이다. 오히려 시뮬레이션에서 염두하지 못한 변수가 훨씬 많을 것이라 생각한다.

Wheel Dynamics

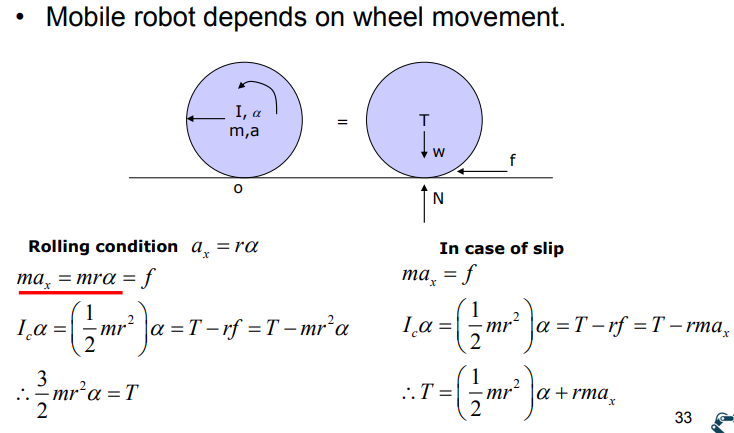
앞서 시뮬레이션에서 노이즈를 준 이유와 실제 모바일 로봇이 원하는만큼 완벽한 주행을 수행하지 못하는 이유중 하나로 Slip이 있다. Slip은 완벽히도 랜덤하고 모델링이 불가능해서 강의에서는 모바일 로봇의 주행에 대해서 저주라고 언급한다. 바닥의 상태, 바퀴의 상태 등 여러 요인이 Slip의 원인이 된다. 이 Slip에 대해서도 간단히 dynamics를 다뤄 봤다.