[Lecture 2] Localization
Updated:
본 포스팅은 양정연 교수님의 SLAM 수업을 Reference로 공부한 내용을 정리한 것입니다.
Mass-Spring-Damper System
본 강의에서는 가장 먼저 위와 같은 mass-spring-damper system을 소개한다. 해당 시스템은 제어 이론을 공부했더라면 한 번쯤을 봤을 기본적인 시스템이다. 로봇의 Localization을 다루는 챕터에서 왜 갑자기 mass-spring-damper system을 언급하는지는 나도 의아했던 부분이지만, 이를 따라가다보면 아주 기본적인 로봇의 Localization 방법론을 알 수 있다.
양 교수님은 이 시스템을 지진계와 연관 지어 설명하신다. 중간 부분을 건너띄고 시작과 결론만을 보이자면 다음과 같이 각 지점에 지진계가 있을 때, 지진계들의 관찰 내용을 한데 모아 최적화를 수행하면 정확한 진원을 추정할 수 있다는 것이다.
mass-spring-damper system의 전달함수와 root locus 등의 제어 이론, 지진계에서 가속도 변화에 따른 출력 등의 내용은 강의에서 상세하게 다뤄주신다.
이와 동일한 방식으로 Beacon-based Localization을 수행할 수 있다.
Beacon-based Localization
위 그림과 같이 어떠한 센서 여러개에서 인식한 결과를 합쳐 현재 로봇의 위치를 추정하는 것을 Beacon-based Localization이라 한다. 앞서 지진계를 예로 들었지만 또 다른 직관적인 예로 GPS를 생각해 볼 수도 있다. 우리는 스마트폰을 들고 현재 위치를 찾으려고 할 때 여러대의 인공위성으로부터 수집한 데이터들을 가지고 현재 위치를 알아낸다. 예를 들어 인공위서 다섯 대에서 정보를 수집한다면, 각 인공위성의 정보 중 겹치는 지역에 내가 존재할 확률이 생긴다. 이러한 존재 확률은 인공위성의 갯수가 늘어날 수록 오차가 줄어들 것이다. Beacon-based Localization은 이렇게 인공위성을 활용한 GPS와 동일한 방법이다.
그렇다면 이 방법은 완벽한 것인가? 물론 아니다. 앞에서 자연스럽게 언급했듯이 반듯이 오차가 존재하기 마련이다. Localization의 정확도를 높이기 위해서는 이러한 오차를 줄이는 것이 중요하다. 오차를 줄이기 위한 방법으로는 최적화 기법을 사용한다.
Gradient Descent Method
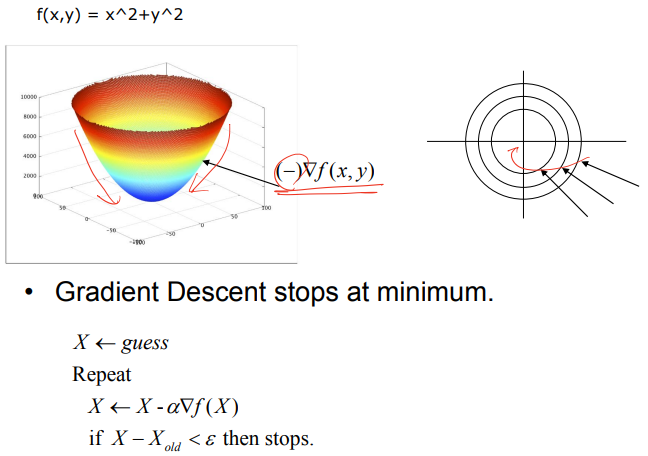
최적화 기법으로는 경사하강법으로 불리는 Gradient Descent 방식을 사용한다. 이는 간단히 말하자면, 기울기가 작아지는 방향으로 연속해서 값을 이동시키는 방법이다. 직관적인 예를 들어보자면, 산 정상에서 하산할 때를 생각하면 이해가 빠를 것이다. 하산을 하기 위해서는 발 끝의 감각에 의지하여 경사(기울기)가 음의 방향을 향하도록 이동한다. 이와 같이 기울기를 이용하여 Local minima를 찾는 것이 곧 경사하강법, Gradient Descent이다.
Gradient Descent를 하기 위해 기울기 함수를 표현하자면 아래와 같다.
이와 같은 기울기 함수를 다음과 같이 원의 형태로 예시를 들어본다면, 진행 방식은 아래 그림과 같다.
추정된 로봇의 위치인 $X$에서 기울기에 비례하도록 오차를 빼 나가면서 local minima에 도달하는 것이다.
이 방식을 Beacon-based Localization에 적용하면 다음과 같다. 먼저 기울기 함수 $f$는 아래와 같이 정의할 수 있다. 이때 $N$은 주변 beacon의 개수, $B_i$는 beacon의 위치(벡터), $d_i$는 $X$로부터 $B_i$까지의 추정 거리(Estimated Euclidean distance)이다. 동시에 아래 기울기 함수에서 $\Sigma$ 내부에 들어가는 것은 오차라고 볼 수 있을 것이다.
이러한 Beacon-based Localization은 실제 코드로 실험해보면 원하는 위치로 잘 찾아가는 것을 확인할 수 있다. 또한 주변 beacon의 개수가 많을 수록, 즉 위 식에서 $N$의 값이 클 수록 오차가 줄어드는 것을 할 수 있다. 하지만 한가지 염두해 두어야 하는것은, $f$의 값이 완벽한 0이 될 수는 없다는 것이다.

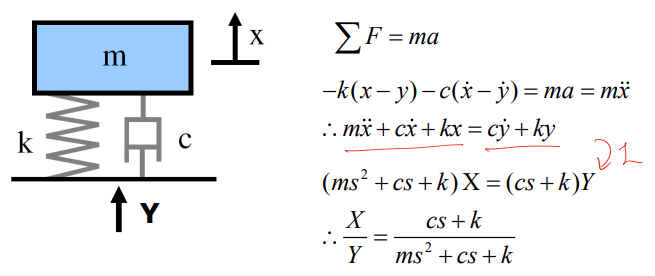

Comments