[Lecture 1] Mobile Robot Kinematics
Updated:
본 포스팅은 양정연 교수님의 SLAM 수업을 Reference로 공부한 내용을 정리한 것입니다.
Mobile Robot
모바일 로봇, 혹은 이동 로봇은 특정 공간에 고정된 로봇이 아닌, 자체적인 동력을 가지고 이동을 할 수 있는 로봇을 말한다. 이와 같은 로봇에 대한 수요는 요즘 들어 급 부상하고 있다고 생각하고, 연구 소재로 많은 기관 및 기업에서 큰 관심을 가지고 있다. 이미 실증이 이뤄지고 있는 로보티즈의 일개미, 집개미나 우아한 형제들의 딜리와 같은 로봇들이 미래의 모습을 상상할 수 있게 해준다. 이러한 모바일 로봇을 보다 제대로 이해해보고자 한다.
모바일 로봇을 공부하기 위해 간단한 모델 하나를 소개하자면 다음과 같은 2-Wheel Robot을 들 수 있다.
위와 같은 모바일 로봇이 원하는 속도를 가지고 회전과 이동을 수행하기 위해서는 많은 요소가 고려되어야 한다.
- Moment of Inertia
- Wheel Dynamics
- System Dynamics
- Disturbance
- Control Theorem
Inertia나 Wheel dynamics, 제어 이론 등은 본 강의에서 많은 시간을 할애하여 언급하지는 않는다. 기본적인 내용이거나, 혹은 제어 이론과 같이 보다 하위단 내용을 파고들고자 한다면 상당히 긴 강의가 될 것이다.
이들에 대한 기본적인 지식이 있다는 가정하에 모바일 로봇 이론에 대해 강의를 진행한다.
Mobile Robot Kinematics
1. Translation
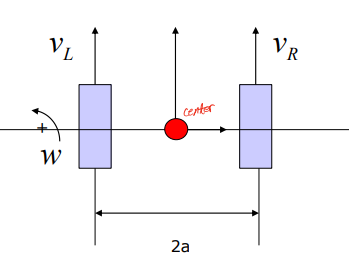
다음과 같이 간단한 2-Wheel Mobile Robot을 가정해보자.
로봇의 중심을 기준으로 좌우, 같은 간격으로 두 개의 바퀴가 위치한다. 이 로봇은 이동할 때 두 바퀴를 굴려 이동할 것이다. 이때 두 바퀴의 선속도를 각각 $v_L, v_R$로 정의했다. 그렇다면 로봇 자체의 선속도는 두 바퀴 선속도의 평균으로 다음과 같이 정의될 것이다.
2. Rotation
위 그림과 같은 모바일 로봇은 두 바퀴의 선속도를 다르게 하여 회전 운동을 할 수 있다. 이는 딱히 설명하지 않아도 당연한 것으로 생각된다. 이제는 로봇의 회전속도를 구해볼 필요가 있다. 먼저 다음의 회전속도와 선속도의 기본 공식을 알고 있어야 한다.
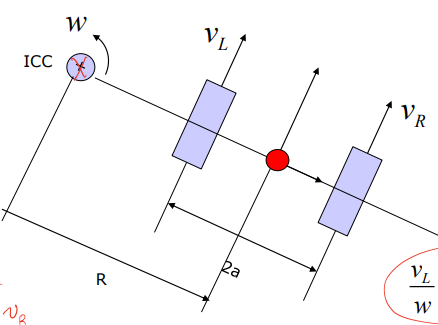
이제 로봇이 회전하는 순간을 도식화하여 그려보자.
강의자료에서는 로봇의 회전 중심을 $ICC(Instantaneous Center of Curvature)$로 명시했다. 로봇이 $ICC$를 중심으로 회전할 때 양측 바퀴에 위에서 언급한 $v=r\times w$ 식을 적용하면 다음과 같이 로봇의 회전속도 $w$를 도출할 수 있다.
3. Differential Drive Kinematics
이제 로봇의 병진속도(Translation)와 회전속도(Rotation)를 알아냈다.
두 식에 대해 세 가지 케이스를 나눠 2-Wheel Mobile Robot이 수행할 수 있는 움직임들을 설명할 수 있다.
case1) $ w=\frac{v_R-v_L}{2a}=0 $
$ v=v_L=v_R $ 인 상황이므로, 로봇은 병진운동만을 한다.
case2) $ v_L=-v_R $
$ w=\frac{v_R}{a}, v=\frac{v_L+v_R}{2}=0 $ 이므로 제자리 회전을 한다.
case3) $ v_L=0 $
$ w=\frac{v_R}{2a}, v=\frac{v_L+v_R}{2}=\frac{v_R}{2} $ 이므로 왼쪽 바퀴를 축으로 회전한다.
다음으로 병진속도와 회전속도 식을 행렬을 사용해 표현해보자.
$ \begin{pmatrix}
v
\\
w
\end{pmatrix}=
\begin{pmatrix}
\frac{1}{2} & \frac{1}{2} \\
\frac{-1}{2a} & \frac{1}{2a} \
\end{pmatrix}
\begin{pmatrix}
v_L \\ v_R
\end{pmatrix}=r
\begin{pmatrix}
\frac{1}{2} & \frac{1}{2} \\
\frac{-1}{2a} & \frac{1}{2a} \
\end{pmatrix}
\begin{pmatrix}
w_L \\ w_R
\end{pmatrix} $
위 식에서 알 수 있는 것은 양측 바퀴의 각속도를 조절하면 로봇의 병진속도와 회전속도를 제어할 수 있다는 것이다.
4. Jacobian
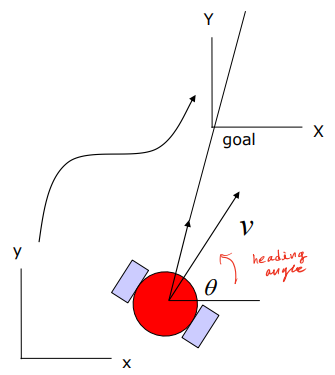
위에서 구한 식을 좌표계에서 보이기 위해 재구성할 필요가 있다. 먼저 로봇의 속도는 다음과 같이 $x$축, $y$축으로 분해하여 표현 가능하다.
동시에 위와 같이 월드 좌표계 위에서 로봇의 pose는 현재 로봇의 위치와 회전 각도로 정의할 수 있다.
이때 로봇의 pose X를 시간에 대해 미분한 것이 한 시점에서 로봇의 속도, 각속도가 된다. 이는 식으로 나타내면 다음과 같다.
$ \dot{X}=
\begin{pmatrix}
\dot{x} \\
\dot{y} \\
\dot{\theta}
\end{pmatrix}=
\begin{pmatrix}
vcos\theta \\
vsin\theta \\
w
\end{pmatrix}=
\begin{pmatrix}
cos\theta & 0 \\
sin\theta & 0 \
0 & 1 \
\end{pmatrix}
\begin{pmatrix}
v \\ w
\end{pmatrix} $
여기서 우변의 $v, w$는 위 식에서 양측 바퀴의 각속도로 얻을 수 있음을 보였다. 이를 모두 정리하면 다음과 같다.
$ \dot{X}=
\begin{pmatrix}
\dot{x} \\
\dot{y} \\
\dot{\theta}
\end{pmatrix}=
\begin{pmatrix}
vcos\theta \\
vsin\theta \\
w
\end{pmatrix}=
\begin{pmatrix}
cos\theta & 0 \\
sin\theta & 0 \\
0 & 1 \
\end{pmatrix}
\begin{pmatrix}
v \\ w
\end{pmatrix}=
\begin{pmatrix}
cos\theta & 0 \\
sin\theta & 0 \\
0 & 1 \
\end{pmatrix}
\begin{pmatrix}
\frac{v_L+v_R}{2} \\
\frac{v_R-v_L}{2a}
\end{pmatrix} $
$ =\begin{pmatrix}
cos\theta & 0 \\
sin\theta & 0 \\
0 & 1 \
\end{pmatrix}
\begin{pmatrix}
\frac{1}{2} & \frac{1}{2} \\
\frac{-1}{2a} & \frac{1}{2a} \
\end{pmatrix}
\begin{pmatrix}
v_L \\ v_R
\end{pmatrix}=
\frac{1}{2}
\begin{pmatrix}
cos\theta & cos\theta \\
sin\theta & sin\theta \\
-\frac{1}{a} & \frac{1}{a} \
\end{pmatrix}
\begin{pmatrix}
v_L \\ v_R
\end{pmatrix} $
$ =\frac{1}{2}
\begin{pmatrix}
cos\theta & cos\theta \\
sin\theta & sin\theta \\
-\frac{1}{a} & \frac{1}{a} \
\end{pmatrix}
\begin{pmatrix}
rw_L \\ rw_R
\end{pmatrix}=
\frac{r}{2}
\begin{pmatrix}
cos\theta & cos\theta \\
sin\theta & sin\theta \\
-\frac{1}{a} & \frac{1}{a} \
\end{pmatrix}
\begin{pmatrix}
w_L \\ w_R
\end{pmatrix} $
$\therefore \dot{X}=
\begin{pmatrix}
\dot{x} \\
\dot{y} \\
\dot{\theta}
\end{pmatrix}=
\frac{r}{2}
\begin{pmatrix}
cos\theta & cos\theta \\
sin\theta & sin\theta \\
-\frac{1}{a} & \frac{1}{a} \
\end{pmatrix}
\begin{pmatrix}
w_L \\ w_R
\end{pmatrix} $
앞선 식과 동일하게 좌우 바퀴의 각속도를 조절하여 로봇의 $x$축, $y$축 속도와 회전 속도를 제어할 수 있다는 결론이 나온다. 두 바퀴의 각속도를 입력으로 하여 로봇의 속도, 각속도 성분이 한 번의 행렬 곱을 통해 정의된다. 이때 이 행렬을 자코비안 행렬(Jacobian matrix)라 한다.
$ J=\frac{r}{2}
\begin{pmatrix}
cos\theta & cos\theta \\
sin\theta & sin\theta \\
-\frac{1}{a} & \frac{1}{a} \
\end{pmatrix} $
또한 이러한 자코비안 행렬을 통해 입력에 의한 출력을 얻어내는 것을 Forward Kinematics라 한다. 이상의 내용들을 정리하여 단순하게 표현하면 다음과 같다.
$ dX=J\begin{pmatrix} d\theta_L \\ d\theta_R \end{pmatrix}=Jd\Theta $
5. Inverse Kinematics
사실상 우리가 원하는 것은 원하는 로봇의 pose 입력으로 주는 것이다. 로봇에게 목표 pose를 입력으로 주면, 로봇은 일련의 과정을 통해 해당 pose에 도달할 수 있도록 양측 바퀴를 제어해야 한다. 이는 앞에서 살펴본 내용과 정 반대이다. 즉, 양변에 자코비안 행렬의 역행렬을 곱해주면 원하는 결과를 얻을 수 있다는 것이다. 하지만 이미 알듯이 자코비안 행렬은 $3\times 2$ 행렬로 역행렬이 존재하지 않는다. 이러한 상황을 타개하기 위해 두 가지 방법이 존재한다.
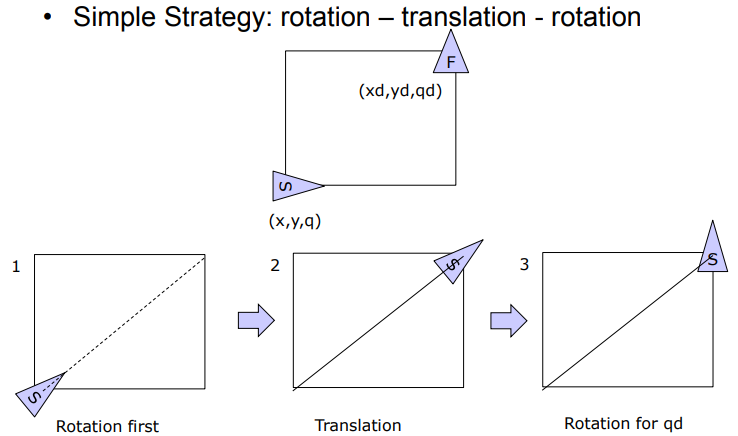
5.1 RTR Method
먼저 간단한 방법으로 로봇의 움직임을 최소 단위로 나누어 실행하는 것이다.
이 그림과 같이 주어진 목표로 향하기 위해 회전과 이동을 별개의 액션으로 수행하는 것이다. 회전 -> 이동 -> 회전과 같이 분리된 움직임을 수행한다면 두 바퀴의 각속도는 서로 같거나, 절대값이 같아져 소거되는 항이 생긴다. 이를 활용하면 다음과 같이 쉽게 양측 바퀴의 각속도를 구할 수 있다.
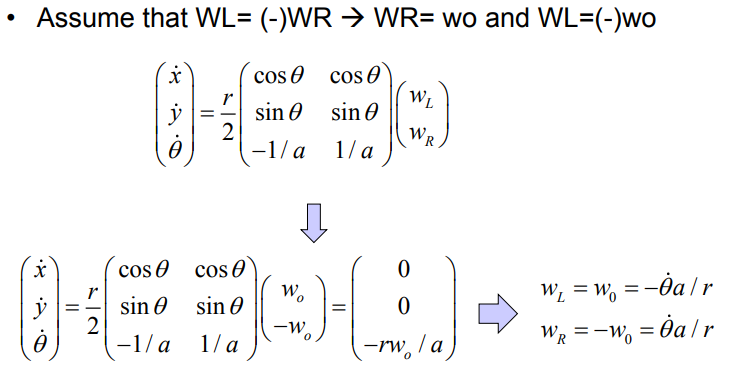
5.2 Inverse Kinematics with optimality
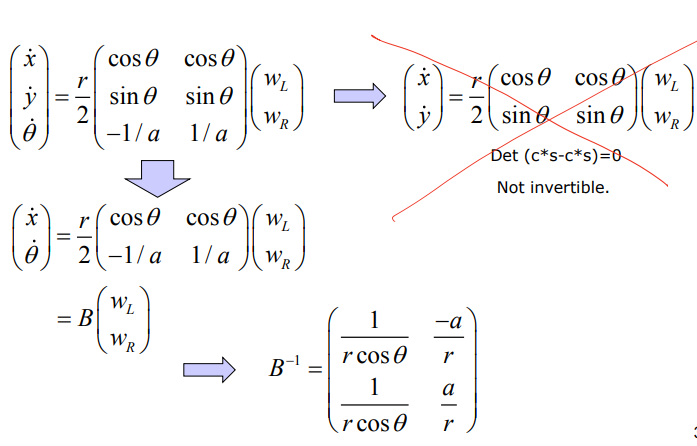
또 다른 방법은 변수들의 독립성을 고려하여 자코비안 행렬을 나눠보는 것이다. $\dot{x}$와 $\dot{y}$는 서로 종속성이 있는 변수들이므로, $\dot{x}$와 $\dot{\theta}$를 선택해 다음과 같이 나눈다. 이때 우변에 곱해지는 자코비안 행렬의 일부를 $B$라고 정의하면, 이 행렬은 $2\times 2$ 이므로 역행렬을 구할 수 있다.
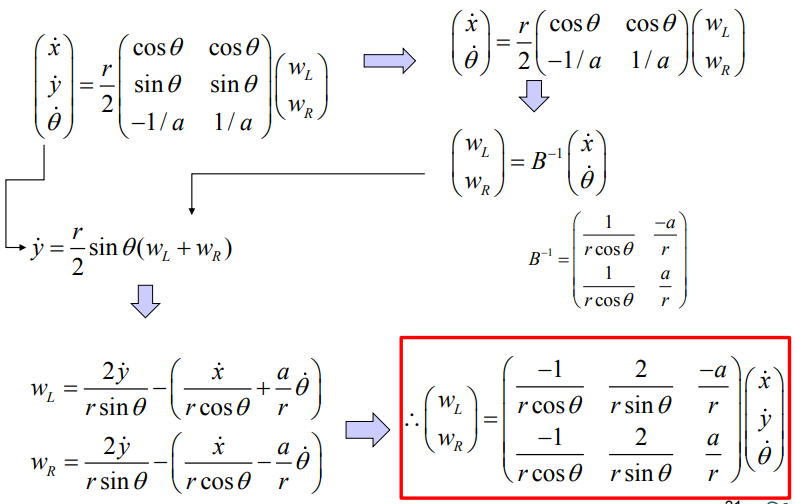
다음으로 $\dot{y}$에 대한 식과 $B$의 역행렬을 곱해 얻어낸 $w_L, w_R$을 연립하여 정리하면 다음과 같은 결과를 얻을 수 있다.
이와 같이 간접적인 방법을 통해 자코비안 행렬의 역행렬을 구할 수 있다. 하지만 이는 확실한 한계를 가진다. 해당 자코비안 역행렬을 사용하여 Inverse Kinematics 문제를 풀고자 한다면, 짧은 이동거리, 한 번의 액션이라는 가정이 필요하게 된다.


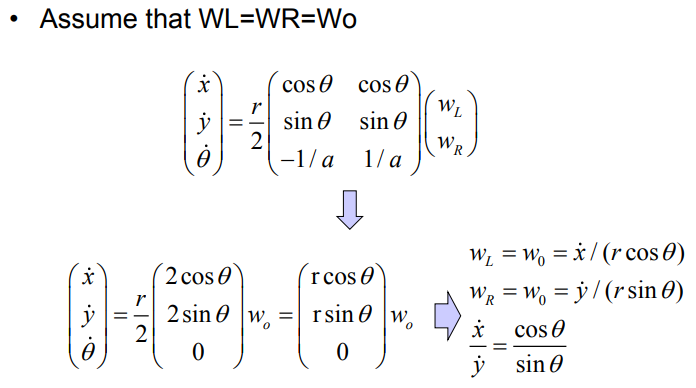
Comments